√画像をダウンロード 円�� 重心 167713-重心の求め方 ���錐
確かに、上の絵で重心を支点にした、力のモーメントはつり合います! 重心を支点とした時の力のモーメントが、必ずつり合うことを覚えておけば、 重心の公式を覚える必要はない ね! 塾長 重心のまとめ 重心は、全重力の作用点 ⇨重心を支点とした重心とは、物体の重さが作用する点です。 普通、重力は一様に作用するので、図形の芯が重心であることが多いです。 今回は重心の簡単な意味、定義、求め方、公式について説明します。 下記の記事を読むと、スムーズに理解できます。 図心ってなに 重心の求め方は一通りではないため、テキストをたくさん見れば見るほど混乱するかもしれません。 今回は、 重心の意味から求め方(3パターン)までじっくり解説していきます。 これを読んで、重心の分野が得意と言えるようになりましょう!
三角形の重心 A Center Of Gravity Geogebra
重心の求め方 円錐
重心の求め方 円錐- 図形の重心 正三角形の重心 では正三角形の重心を求めてみましょう。 次のような正三角形を考えます。 そしてこの三角形の\(x\)方向の重心\(x_G\)は $$ x_G = \frac{a}{2} $$ にあることは図からわかります。 では、\(y\)軸方向の重心\(y_G\)を少し計算して求めてみ三角錐の重心から円錐の重心へ 三角錐の重心は底面から高さ4分の1の所にあります。 円錐は無数の三角錐に分割することができます。 それらの三角錐の重心の重心はどこにあるのでしょうか?



Base7
本当にラストにします‥‥この底面の半径d高さhの円すいの重心位置を教えてください!式となんでその式になるかも教えてください! 数学 締切済 教えて! 重心の上に来る小さい円錐と元の円錐は相似形。 まずは直円錐(傾きのない円錐)を イメージしてください。 直円錐の場合の重心はどんなに 高さがあっても底面から4分の1の 高さに重心があります。 立木の場合、そこに枝や葉の重さを 加えた時の重心は樹高の半分かそれよりも わずかに下になります。平面形状の重心の算出式は、ミスミfa用メカニカル標準部品カタログの技術データに21種類の形状について解説されています。 (3)立体形状 7)直方体 8)円錐と角錘
半円板は重心が 重心まわりの慣性モーメントが と少し複雑な結果になるので慎重に計算していきましょう。 これまで剛体の問題は「 力学斜面を転がっていく剛体 」や、「 慣性モーメント円柱が段差を乗り上げる条件 」などでやってきたように 1 円弧の重心 以下の円弧の重心を求める。 2 弓形の図心 以下のような半径10cm、中心角90°の弓形(ハッチング部分)の図心を求める。 3 半球と円錐をくっつけた物体の重心位置について 半球と円錐をくっつけた以下のような物体の重心が0点よりも下にあるためのrとhの関係を求める。 円錐の体積の求め方がわかる3つのステップ つぎの例題をときながらみていこう! Step1 円錐の「底面積」を計算するっ! まずは円錐の底面積を計算してみよう。 円錐の底面は「円」になっているね。 ってことは、 円の面積の公式 をつかって
円錐の体積を計算するには、円錐を微小な厚さの円盤の集合と見立てて計算します。 微小な厚さの円盤の体積を\(\Delta V\)とすると体積は \ V = \sum \Delta V \ という風に書けます。 微小な円盤の半径と体積 頂点を原点にして、底面に垂直な軸を\(z\)軸にします。円錐台の体積 大変助かりました。 エンジンのシリンダーヘッドのスキッシュエリアの体積を求めるのに使わせて頂きました。 こども園の園庭に作るつきやま盛土の体積を求めるために役立ちました。 バケツの中に降り積もった雪の体積を測定したくてこのページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。 お使いのブラウザでは JavaScript が無効になっています。 当サイトは数式表示に JavaScript を利用しているため、これを無効にしているとページが正しく表示されません。



1



Base7
円錐台(えんすいだい、英 circular truncated cone )は、底面が円である錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される立体である。 重心の求め方から応用問題まで徹底解説! │ 受験スタイル 例題付き重心って何? 重心の求め方から応用問題まで徹底解説! スポーツで、「重心」という言葉を聞くことがあると思います なんとなく物体の中心というイメージをもっているのでは重心 高校物理では, 質量はあるが大きさは無視できる という 質点 についての議論がもっぱらである しかし, 現実の物体はゼロでない大きさを持ち, 物体内部で質量の分布に 斑 このような現実的な物体を議論する場合において, 著しい特徴を持つ点, 重心




図形の重心を解析的に求める方法 理系のための備忘録




Amazon Co Jp 交通安全通りコーン 道路交通円錐 非常に低い重心を持つ強くて丈夫な自重の安全円錐形 Size 60cm 車 バイク
重心の一覧(じゅうしんのいちらん)を記述する。 幾何学における重心とは、図形内における1次のモーメントの総和が0になる点である。 これは、力学において均一な密度を持つ物体の重心と一致する。 一般的な重心の位置 図形が点対称の場合、重心は対称の中心と一致する。 と書けます。 円錐の質量Mは、 =k (H^2h^2)/2 =2/3* (H^2Hhh^2)/ (Hh) と変形すると、重心位置は、小円の中心と大円の中心を (2Hh) (h2H)に内分する点であることが分かります。 細かな解説までつけていただいて誠にありがとうございます。 非常に助かりました三角形の五心の重心座標 重心座標のメリット1:五心のデカルト座標は複雑で覚えたくありませんが, 重心座標は美しくて覚えやすい&扱いやすい です。 そのため五心が絡んだ問題を座標計算で解くときに威力を発揮します。



1
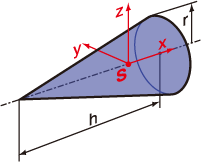



4 ステップ2 負荷の動作 9 マクソンジャパン ドットコム
台形の重心公式: a 2 b 3 ( a b) h を導出してみます。 重心の定義は、 断面一次モーメント÷面積 です。 面積は、 台形の面積を求める公式 より、 S = 1 2 ( a b) h です。 (下底まわりの)断面一次モーメントは、 y における横棒の長さ が a ( b − a) y h上式の通り、台形の重心は、上辺の長さ、下辺の長さ、高さが決定すれば計算できます。 例えば、 h=3 a=5 b=2 のとき、y=1286です。下図をみてください。下辺の長さが大きい台形ですね。よって、重心が中心より下側に移動することが想像できると重心を通る軸まわりの慣性モーメントは、$\dfrac{1}{3}M(a^2b^2)$ ただし、横の長さを $2a$、縦の長さを $2b$ としました。 一様な長方形・正方形の慣性モーメントの2通りの計算 円盤の慣性モーメント: 重心を通る軸まわりの慣性モーメントは、$\dfrac{1}{2}Mr^2$




円錐の重心はどこにあるの 町人思案橋 クイズ集




写真のような円錐を宇宙空間のような場所で回すとします 重心のズレ 物理学 教えて Goo
ご意見・ご感想 計算方法だけでなく、WEB上で計算までして貰えるとは思わなかったし、そもそもこの形の名称が「円錐台」と呼ぶことも知らなかったので勉強になった。 嬉しい誤算だった。 このサイトを作ってくれた人(達)に感謝します くり抜き図形の重心の求め方とは 重心の公式は紹介されていますが大事なのは 重心の性質を理解することです。 重心のポイントは 「質量の代表点」 ということです。 質量の代表点ということから、重力に関する様々なことを代表するのです(すごい重心の求め方について その2 (1)高さh,底面の半径rの円錐の場合 (2)半径rの半円球の場合




工業力学の問題で息詰まってます 問題 下図のような均質な物体の重心の位 Okwave
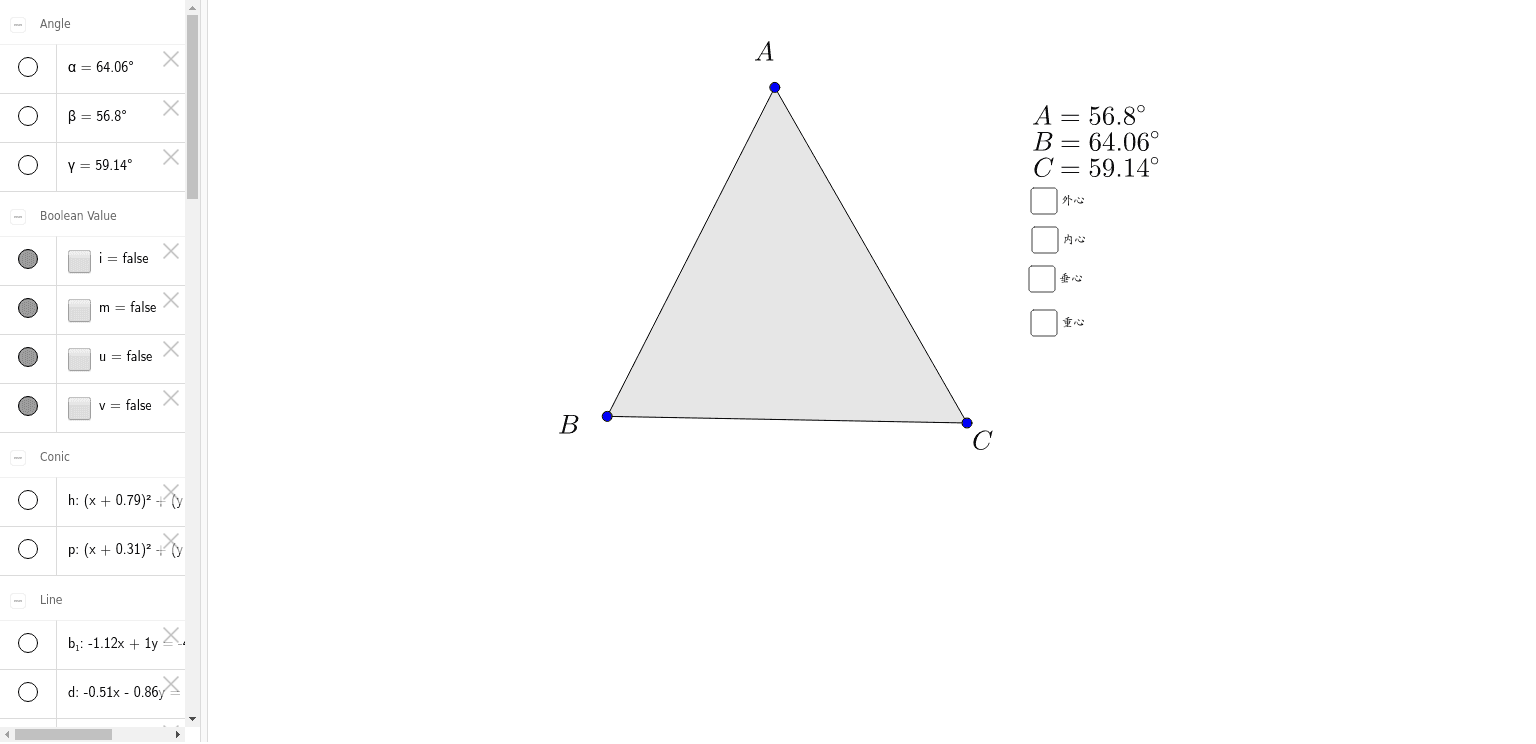



三角形の外心内心垂心重心 Geogebra
円錐と阪急の重心の位置 2242 円錐の重心の位置が側面から頂点までをhとすると 重心G(x、y)はy=1/4×hになります。 また、半球は半径r、重心(x、y)とすると y=3/8×rになります。 なぜこのような式が導かれるのでしょうか? 教えて下さい。半径r,高さhの一様な円錐 の重心の位置を求めよ r h 中心軸上にあることは明白 なので,その位置を求める この線上にある 工学院大学の学生のみ利用可:印刷不可:再配布不可 加藤潔 18 24円柱の重心を通る対称軸に関する慣性モーメントの計算 半径が 、高さが で質量は とする円柱を考えます。 この円柱に対する 軸、 軸、 >軸まわりの慣性モーメントをそれぞれ とします。 を使います。




図形の重心を解析的に求める方法 理系のための備忘録




高校入試対策 知っていたら得 プリン型 円錐台 の表面積を10秒で解く方法 勉強 Youtube スタディチューブ
台形を2つの三角形に分け、その重心を結ぶ直線とAD、 BCの中点を結ぶ直線MNの交点 半円筒形は、物体の外側に重心が位置する。半円筒形を 小さく分割し、分割したそれぞれの重心の合力により 重心位置を求めると、右の図のような位置になる。 円錐の表面積の求め方がわかる3ステップ 円錐の表面積は3ステップで計算できちゃう^_^ つぎの例題をときながらみてみよう。 半径3cm、母線の長さが10cmの円錐の表面積を10秒以内に計算して。 Step1 底面の「円周の長さ」を計算したる まずは底面の「円周 慣性モーメントの導出:円錐 以下のような円錐の慣性モーメントを求めます 密度はρ、質量はmとします まずはz軸まわりの慣性モーメントを求めます 以下の図のように円錐をz軸に垂直な面でスライスします &



2




円錐と半球の重心 ウソの国ー詩と宗教 戸田聡
「三角錐の重心Oの位置は、その高さの4分の1になります。 」 以下に、三角錐の重心の性質の簡単な求め方を示します。 上の図のように、三角錐の重心を3次元座標の原点Oにして考えま問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。



Kadai78



3



積分による重心位置の求め方 わすれなぐさ



視覚学会05年夏季大会用



立体の体積 容積および諸数値
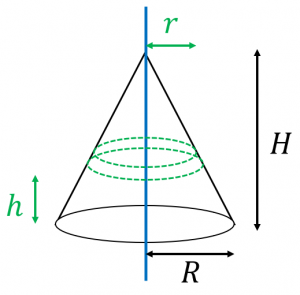



一様な円柱と円錐の慣性モーメント 具体例で学ぶ数学




本当にラストにします この底面の半径d 高さhの円すいの重心位置を教 数学 教えて Goo




三角形の重心 A Center Of Gravity Geogebra



4 ステップ2 負荷の動作 9 マクソンジャパン ドットコム




1円スタート Amadana 加湿器 Fh309bk Amadana アマダナ Air Care Diffuser エアケア ディフューザー Fh309bk 超音波式 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com
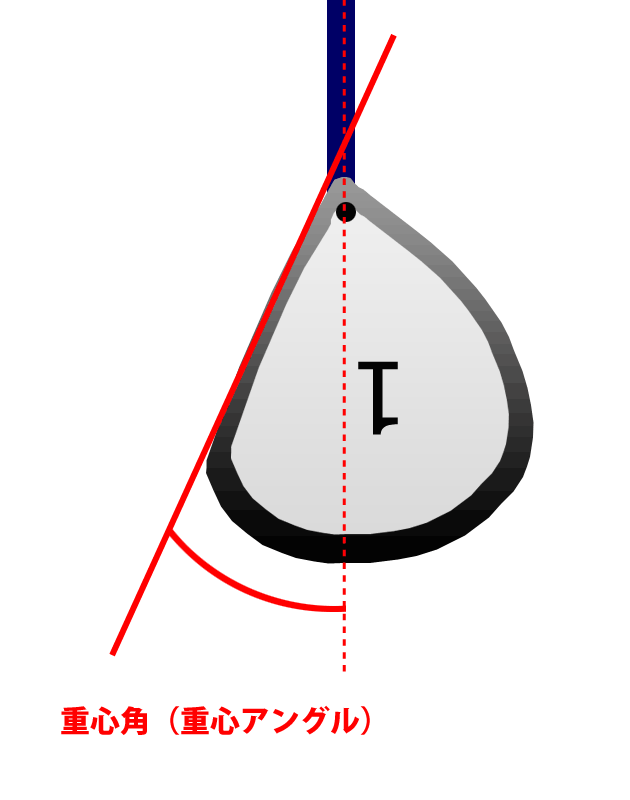



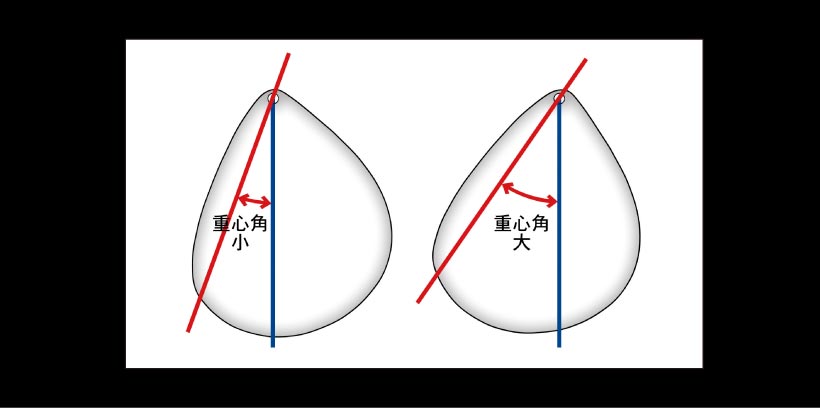
重心角 重心アングル 飛ぶドライバー 22年 飛距離を追求するブログ
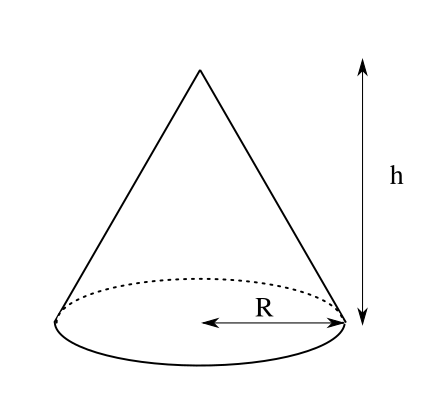



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目




図形の重心を解析的に求める方法 理系のための備忘録



Www1 Meijo U Ac Jp




中学受験算数 円すいの側面上の最短距離の問題 Stupedia



2



Fast 130 Carbon Grips グリップス
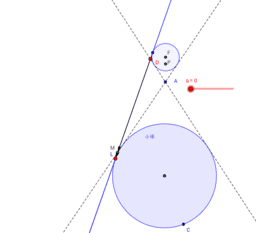



アポロニウス円錐曲線論 Geogebra




中学受験算数 円すいの側面上の最短距離の問題 Stupedia



重心を求める 物理のかぎしっぽ



多角形の面積 重心 図心 断面n次モーメントの公式と 向き 頂点列の回転方向 の判別方法
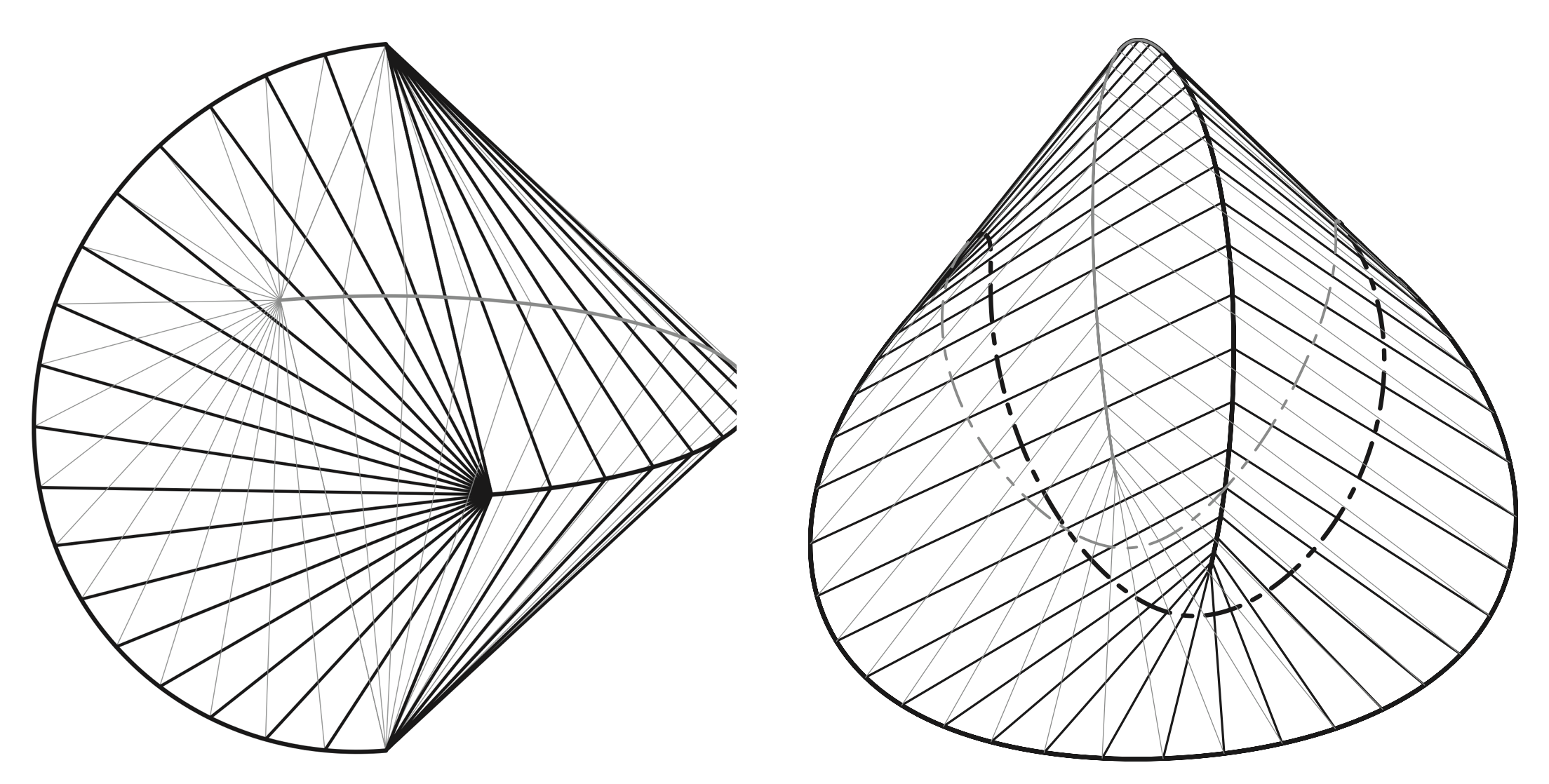



錐体の体積公式と等高重心立体に関する考察 平田浩一 ぼのぼ の ブログ
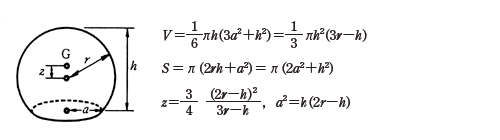



立体の体積 V 表面積 S または側面積 F および重心位置 G 球欠 P12



Math 回転体の体積 表面積とパップス ギュルダンの定理 働きアリ



円錐台の体積を求める問題です 重心は中心軸にある 下の円の中心を Yahoo 知恵袋




高校入試対策数学 空間図形問題 円錐の表面積 重心 三角錐に内接する円錐 高さを求める 体積 三平方の定理 特別な直角三角形の問題 Youtube
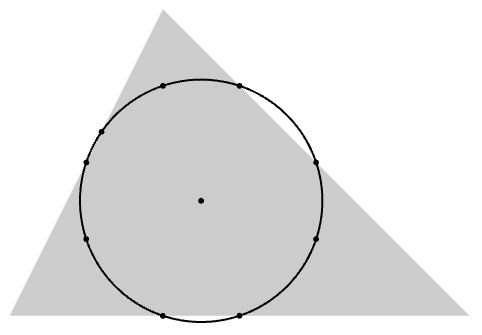



Trianglecenter Wolfram言語ドキュメント




Amazon Co Jp 交通安全通りコーン 道路交通円錐 非常に低い重心を持つ強くて丈夫な自重の安全円錐形 Size 60cm 車 バイク
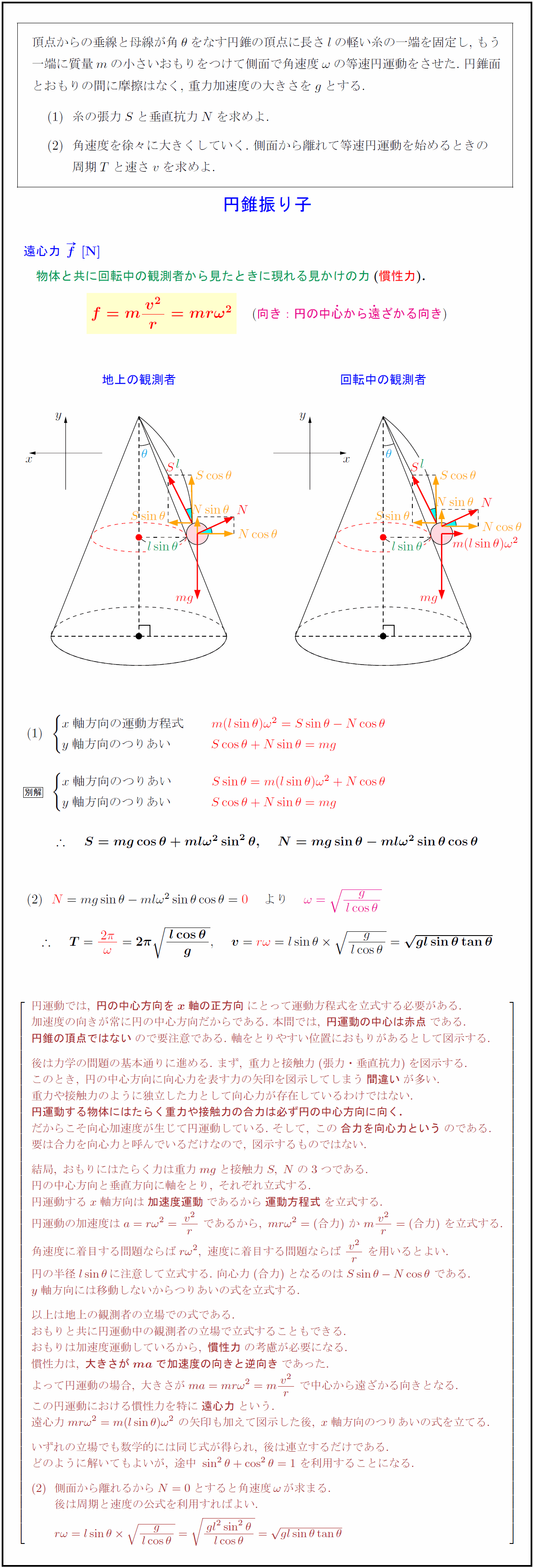



高校物理 円錐振り子と遠心力 水平面内の円運動 受験の月



Base7



重心座標による図形の方程式




質問 大学 物理 円錐の慣性モーメントの求め方 回転軸が 頂点oを 物理学 教えて Goo




慣性モーメントの導出 円錐



2



Base7



正三角形の定義は 面積公式 高さや重心についても解説 受験辞典



Base7



力学の問題です 半球の上に円錐があり中立のすわりになった Hとrの関係を Yahoo 知恵袋




正三角形の重心が中線を2 1に内分するのはなんでだっけ 数学について考えてみる



重心を求める 物理のかぎしっぽ



Base7




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学



添付の円錐台の側面板の重心の求め方を教えていただけないでしょうか Yahoo 知恵袋
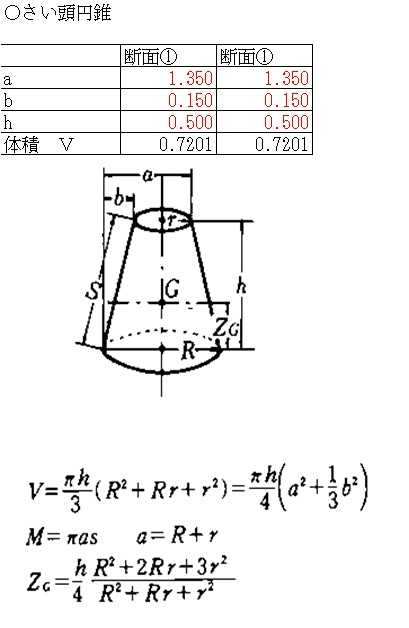



土木設計 体積の算出 晩酌生活 楽天ブログ



円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典



Kadai78



色々な物体の慣性モーメント1 物理のかぎしっぽ



Misc Mathematics Lecture




楽天市場 南ウキ キングモデル 円錐ウキ チヌ グレ フカセ釣り用 ウキ 超低重心モデル ライフジャケット釣具アクアビーチ
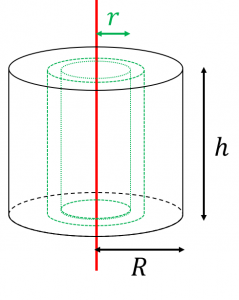



一様な円柱と円錐の慣性モーメント 具体例で学ぶ数学
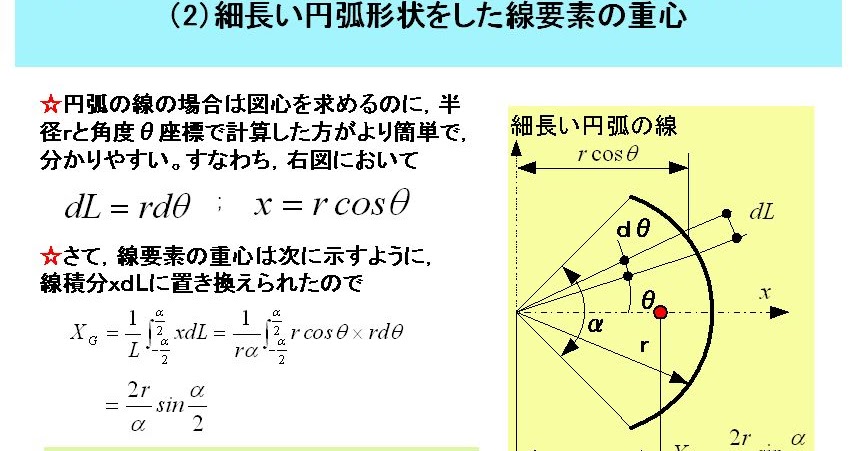



M Sudo S Room 再掲示 部分円弧の重心位置を求める




M Sudo S Room 円錐の側面体 円錐台の側面体の慣性モーメント




超軽量 アルミ カーボンポール 海外限定 ストック ポール トレラン シナノ Sinano 2本1組 カーボンw Fast 130 105 130cm ブラック トレッキングポール
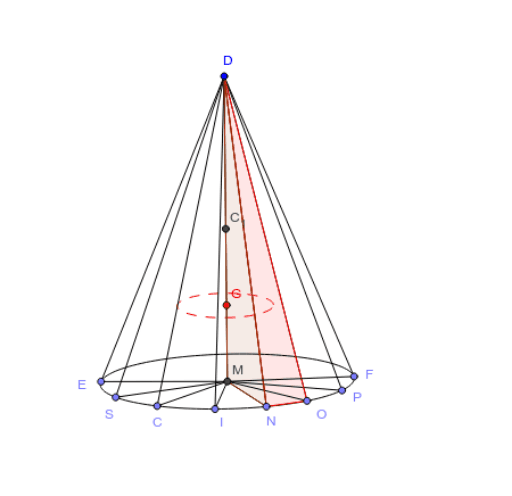



円錐の重心 Geogebra
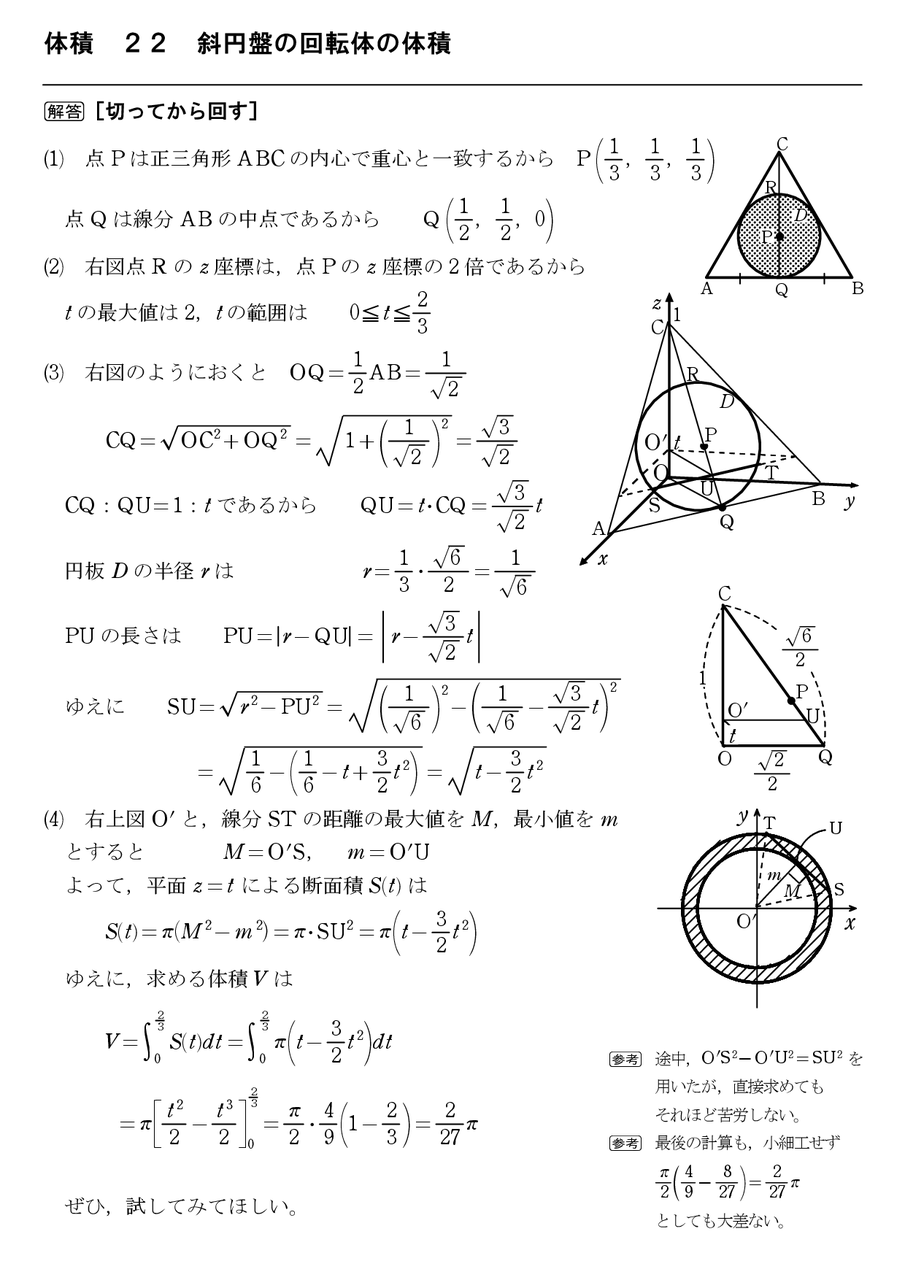



体積 27 円錐の回転体 怜悧玲瓏 高校数学を天空から俯瞰する



半球に半径が同じで高さが半径の2倍の直円錐をくっつけた図形の重心の求め方を教え Yahoo 知恵袋
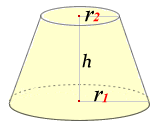



みんなの知識 ちょっと便利帳 円錐台の表面積を計算する
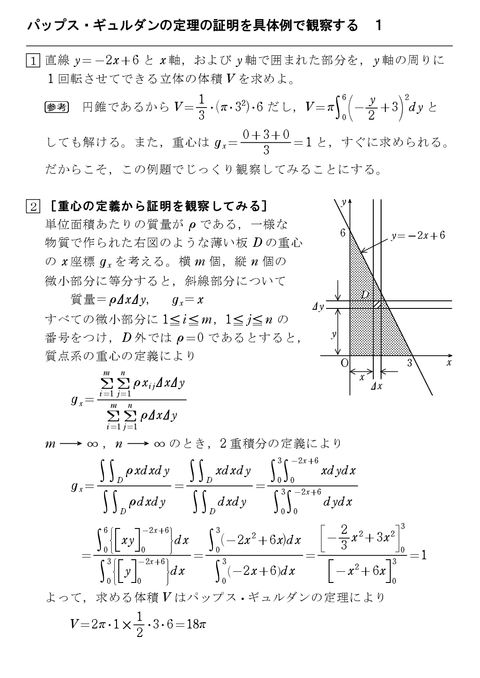



数学iii 怜悧玲瓏 高校数学を天空から俯瞰する



立体の重心次の立体の重心ってどうやって出せばいいですか 円錐台だ Yahoo 知恵袋



1
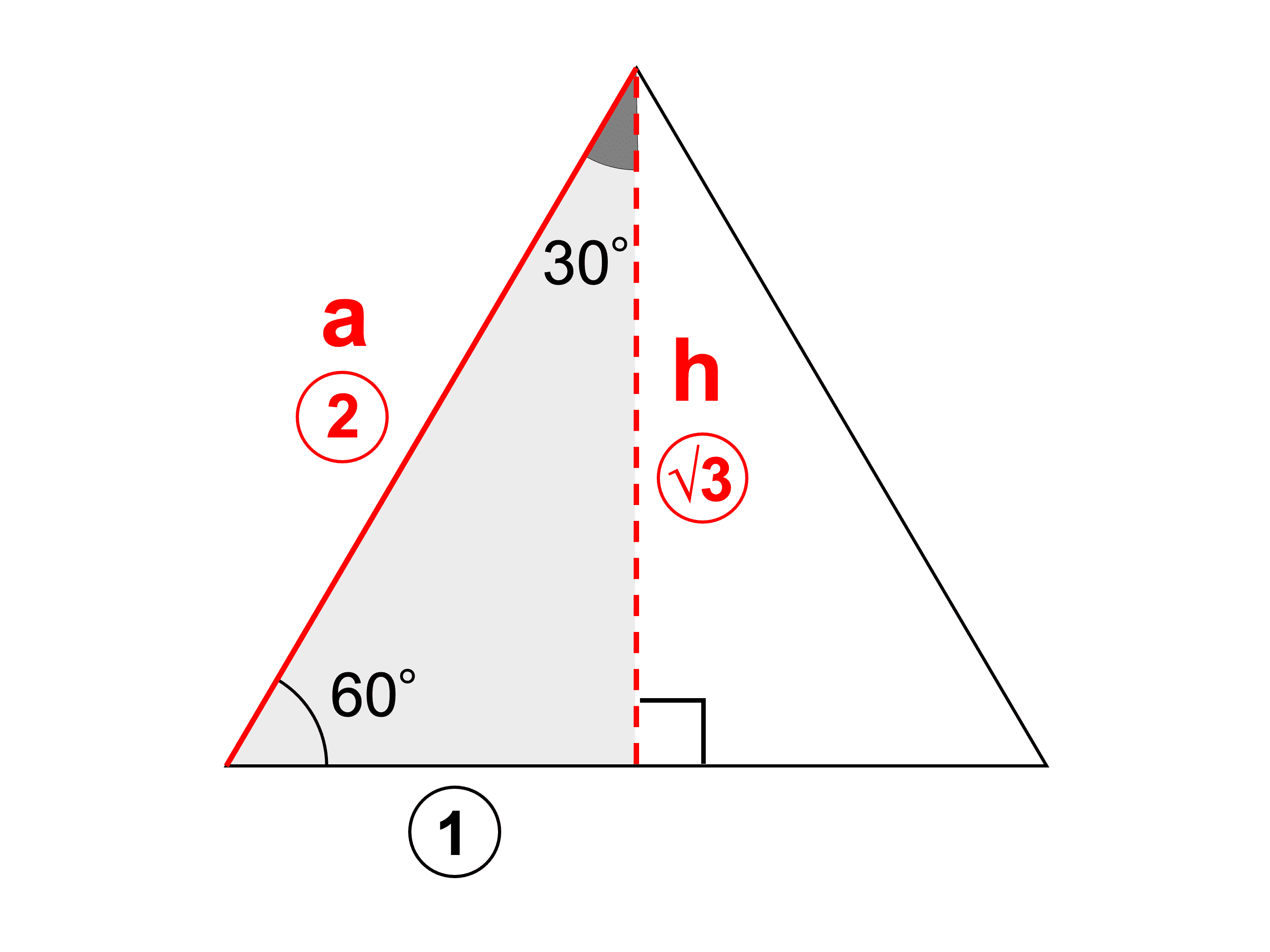



正三角形の定義は 面積公式 高さや重心についても解説 受験辞典



博物館だよりno 48 話題提供
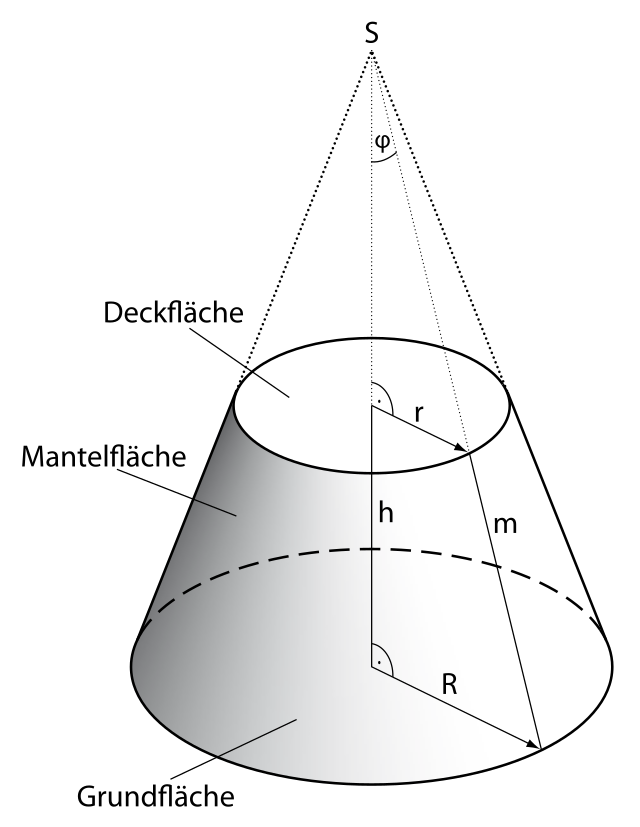



円錐台 Wikipedia




重積分 重積分について 問題を解いてください 形状d物体の密度がr X 数学 教えて Goo



タイリスト ダンロップ ブリヂストン ちょい旧ドライバー性格診断 ゴルフサプリ



林業の数学 Geogebra




重心 Y社長の釣士道日記part2
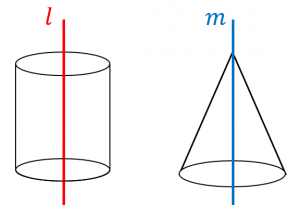



一様な円柱と円錐の慣性モーメント 具体例で学ぶ数学
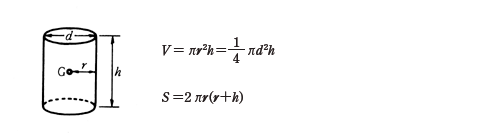



立体の体積 V 表面積 S または側面積 F および重心位置 G 直円柱 P12



Kadai78
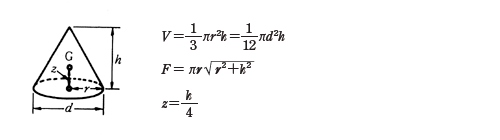



立体の体積 V 表面積 S または側面積 F および重心位置 G 直円錐 P12




立体の体積 V 表面積 S または側面積 F および重心位置 G 角錐台 P12




重心を計算して求める 5 Youtube




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




大根をふたつに切る問題 細いほうがお得 それとも太いほうがお得 町人思案橋 クイズ集



重心を求める 物理のかぎしっぽ
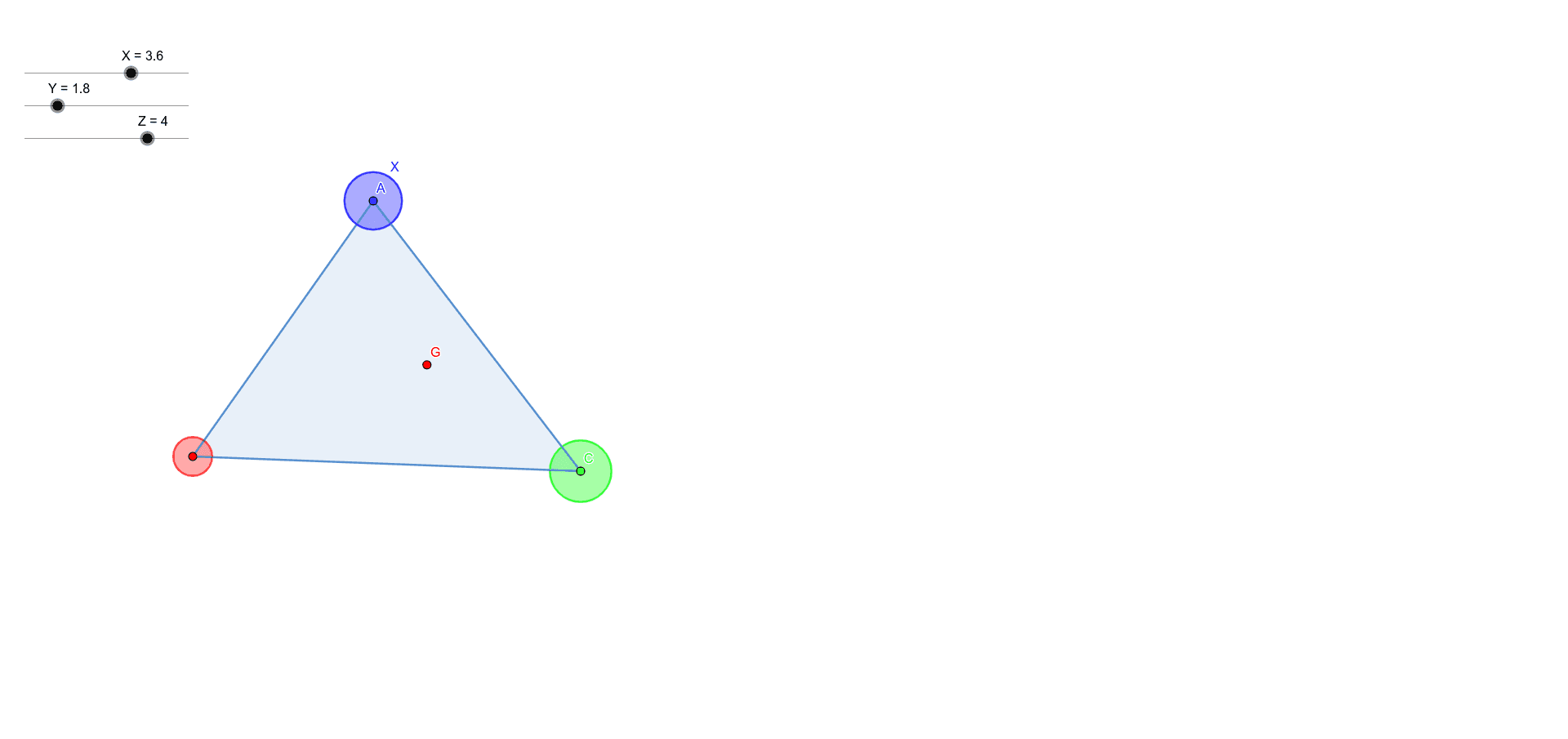



三角形の重心 重さあり Geogebra



重心を求める問題で円錐の体積 底面積 高さ 3円錐の重心の位置 高さ 4を Yahoo 知恵袋




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学



重心を求める 物理のかぎしっぽ




M Sudo S Room 円錐台の慣性モーメントの導出法
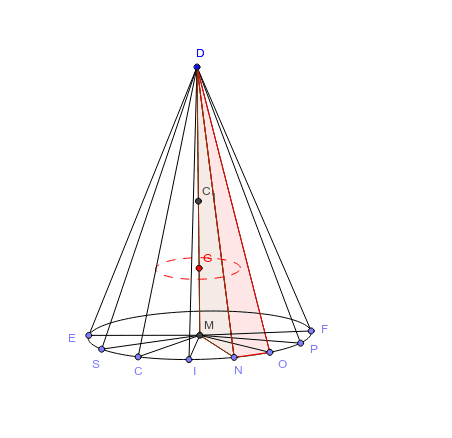



円錐の重心 Geogebra




図形の重心を解析的に求める方法 理系のための備忘録




重心の話




基本形状の重心 機械工学と自動機設計 9 技術情報 Misumi Vona ミスミ




中学受験算数 円すいの側面上の最短距離の問題 Stupedia
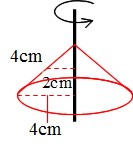



Math 回転体の体積 表面積とパップス ギュルダンの定理 働きアリ



デブはターン中に重心を低くすることに人一倍努めた方がいいかもしれない Skiing Fatman



重心の求め方を教えてください 図のような円錐面の重心のy Yahoo 知恵袋



4 ステップ2 負荷の動作 9 マクソンジャパン ドットコム



コメント
コメントを投稿